It took me a long time to grok representable functors (Chapter 14 of Category Theory for Programmers), so I hope this post will help anyone who’s also struggling. It’ll be a bit silly if I try to motivate everything from scratch, so I’ll assume some familiarity with:
- Morphisms
- Isomorphisms
- Functors
- Hom-functors (or reader functors)
Here we go.
A representable functor is a functor which is isomorphic to the hom-functor.
To unpack that statement, we must first understand how functions and data are really two sides of the same coin.
Imagine a Postgres database storing user data. To keep things simple, let’s say we’re just storing names:
CREATE TABLE "user" (
id SERIAL PRIMARY KEY,
name TEXT NOT NULL
);
localhost=# select * from "user";
id | name
----+------
1 | Adam
2 | Eve
(2 rows)Given an id, we can lookup the user’s name.
Now, it’s not too much of a stretch to imagine converting this Postgres table wholesale into a function that looks like the following:
def findUsernameById(id: Int): String = {
if (id == 1) "Adam"
else if (id == 2) "Eve"
...
}It sounds contrived, but hopefully you can see how functions are really just compact representations of data. Some people try to use terms like memoization — that once you compute a function with some set of arguments, you can store it, and that is the same thing as looking up a map by key.
Since functors can be thought of containers for data, then for a container to be isomorphic to the hom-functor is to mean that this container can “do” whatever the hom-functor can.
Let’s see an example of a functor which is considered representable: the Stream functor.
case class Stream[X](h: () => X, t: () => Stream[X])Notice that a stream, as compared to a list, cannot be empty, and does not have a definite length.
Let’s also go ahead and define the functor and hom-functor (named here more canonically as ReaderFunctor):
trait Functor[F[_]] {
def map[A,B](f: A => B): F[A] => F[B]
}
def ReaderFunctor[E](r: E => _) = new Functor[({ type F[X] = E => X })#F] {
def map[A, B](f: A => B): (E => A) => (E => B) = { r => r andThen f }
}Then, we define a Representable trait like so:
trait Representable[F[_]] {
type A
def tabulate[B](f: A => B): F[B]
def index[B](f: F[B]): A => B
}We’ll explain more about tabulate and index in a bit, but notice first of all that the Representable trait contains an abstract type member A. This will be our fixed reference point in the category of programming types.
And so, we can implement the Stream functor as a representable functor, using Int (assume non-negativity) as the concrete type for A:
def representableStream = new Representable[Stream] {
type A = Int
def tabulate[B](f: A => B): Stream[B] = {
Stream[B](() => f(0), () => tabulate(f compose (_ + 1)))
}
def index[B](f: Stream[B]): A => B = f match {
case Stream(x, xs) => {
n => if (n == 0) x() else index(xs())(n - 1)
}
}
}And if you stare at this implementation long enough, what you’ll see is that tabulate somehow takes a given function f, and “maps” out all results of that function for every input integer 0, 1, 2…, and “stores” that as a stream. Or at least you can think of that way, since it doesn’t actually do the (infinite) computation eagerly, it “stores” it in the tail of the stream.
And index is the inverse of that — it takes a stream and unravels it as far as is needed to find the nth item in the stream, which contains the answer to the input n.
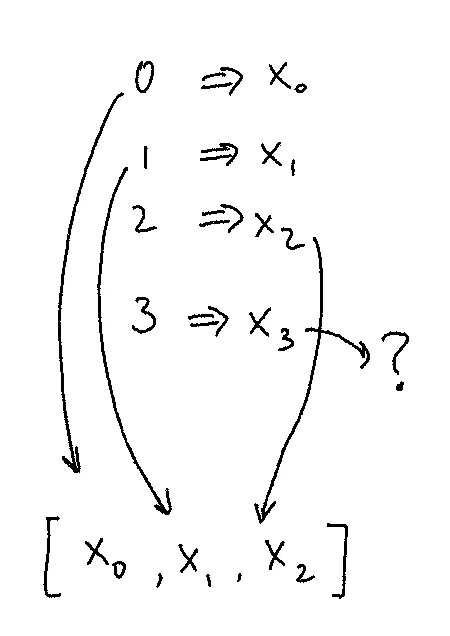
Visually, it looks like this:
We have a function, represented here as a lookup table:

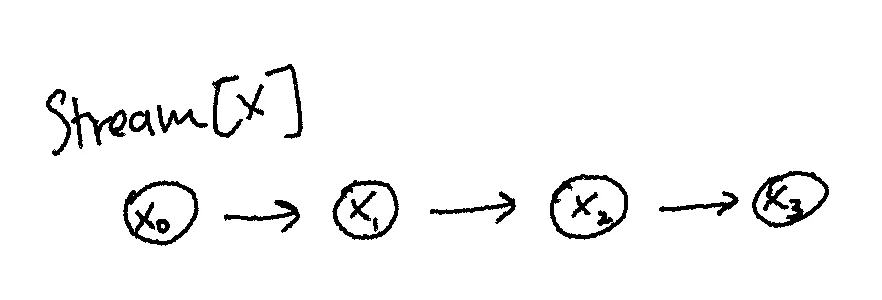
and we have a Stream[X] for some type X:
They are really the same thing:
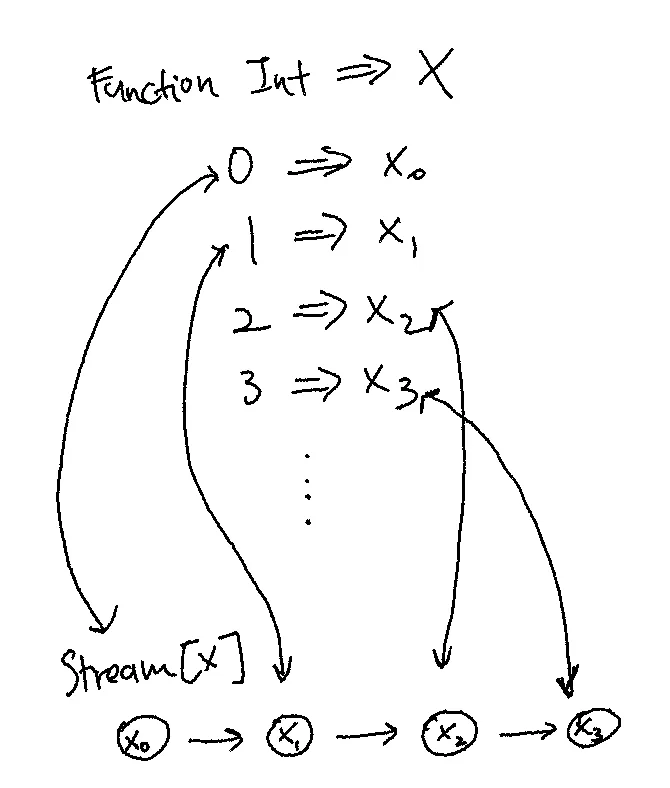
Note the bi-directional arrows. We can go between both representations losslessly.
In some sense, what we’re trying to say is, for some function that takes a (non-negative) integer and returns some x in X, a Stream[X] is the same thing. They are isomorphic. tabulate compose index should be the identity function.
Let’s look at a smaller example. Say we have a Pair type, which contains 2 values of some type A:
case class Pair[A](a: A, b: A)If we use Boolean as the “key” type, Pair is representable, since there are only two possible values for such a function Boolean => B. We arbitrarily choose false to represent the first item in the Pair, and true to represent the second item in the Pair.
def representablePair = new Representable[Pair] {
type A = Boolean
def tabulate[B](f: A => B): Pair[B] = {
Pair[B](f(false), f(true))
}
def index[B](f: Pair[B]): A => B = f match {
case Pair(a, b) => {
n => if (n) f.b else f.a
}
}
}Here, tabulate converts a function Boolean => B into a Pair:
scala> representablePair.tabulate((x) => if (x) 1 else 2)
val res0: Pair[Int] = Pair(2,1)And index converts a Pair into a function Boolean => B (here B is a string):
scala> val f = representablePair.index(Pair("A", "B"))
val f: Boolean => String = $anon$1$$Lambda$1197/1238209644@57cabdc3
scala> f(false)
val res2: String = A
scala> f(true)
val res3: String = BAnd now circling back to the book, we have:
For F to be representable we require that: There be an object α in C; one natural transformation α from C(α, −) to F; another natural transformation, β, in the opposite direction; and that their composition be the identity natural transformation.
The natural transformation α here is tabulate, and β is index. The hom-set C(α, −) represents the set of all mappings, and there is a natural transformation from Reader[A] to Stream[A].
As an extension, note that the List functor [] is not representable, because a list may be empty or too short.